最近在QQ群里看到了下列一则消息:
豆瓣在网页和APP中加入盲水印 可追踪截图用户
豆瓣在15日于其网页版标题下方加入了一行小字,内容是uid、tid和截图时间。这些文本颜色与网页背景色大体接近,肉眼无法直接分辨,如果有人截图通过调节对比度就可以显现出来。豆瓣可以轻松追踪截图者是谁。
在被曝光后豆瓣已将该部分设置为禁止选中。另外豆瓣早在2021年已经在其App中加入了类似功能。
隐写技术并不是新鲜事,其它互联网公司也早有应用,甚至更加先进。
在此前阿里巴巴月饼事件中泄露内网截图的员工虽然对图片做了处理,但是依然可以通过频域手段添加的数字盲水印精确定位到泄密员工。知乎用户 fuqiang liu 经过测试,使用涂抹,剪切,放缩,旋转,压缩,加噪,滤波等手段无法过滤这种盲水印,唯一的办法是对屏幕拍照。但是,依然可以通过文本间距等手段区分不同用户。审查者在这方面有很多技术选项。
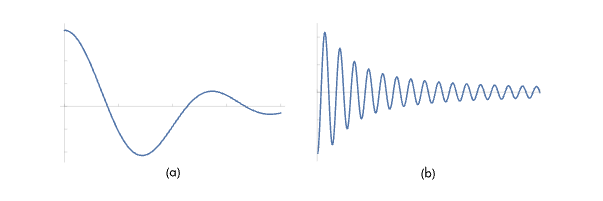
有不少同学十分好奇其中提到的“通过频域手段添加的数字盲水印”是如何实现的。对于初学者而言也确实很难将一张图片与所谓的频率联系起来,那么到底什么是数字图像的频域分析呢?
傅立叶变换
引用一段Wiki对于傅立叶变换的介绍: