正交投影&透视投影
Let's do some math.
由于我们在计算机中的三维图像最终都是需要渲染到屏幕上的,所以我们需要对其进行一次投影的操作,首先假定我们的坐标为右手系,我们首先在\((0,0,0)\) 原点坐标处放置朝向\(-z\)方向,上方为\(y\)轴方向的摄像机,需要得到的图像的大小为 1x1(假设下的理想情况)。现在,有两种投影方式可供选择:
正交投影 Orthographic Projection
虽然这并不是我们最终希望使用的投影方式,但是正交投影在许多场景如 2D 游戏、工程制图等都得到了较为广泛的应用。
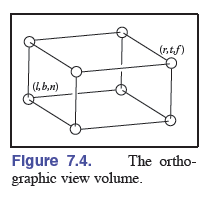
上图为一个典型的正交投影,我们将一个图像等比例地以平行线投射到我们的摄像机采集面(即最终屏幕显示)上,我们并不希望 挪动我们的坐标系或者摄像机,因为这样会导致其他物体的相对摄像机位置改变,于是我们采用将物体“挪动”到原点的方式来产生 最终的图像。于是总共需要进行两次变换:将物体挪动至原点,按 1x1 的目标画布大小进行放缩。
我们假设这个物体为一个正方体(其实所有的物体都可以抽象地看作一个个小立方体),其前、后、上、下、左、右六个面距离立方体中心的距离为\(n, f, t, b, l, r\)(由于摄像机看向\(-z\)方向,这里规定\(n\gt f\)根据前面的齐次坐标变换公式,可以得到如下的变换矩阵:
\[ M_{ortho} = \left[\begin{matrix} \frac{2}{r-l} & 0 & 0 & 0\\ 0 & \frac{2}{t-b} & 0 & 0\\ 0 & 0 & \frac{2}{n-f} & 0\\ 0 & 0 & 0 & 1 \end{matrix}\right] \left[\begin{matrix} 1 & 0 & 0 & -\frac{l+r}{r - l}\\ 0 & 1 & 0 & -\frac{t+b}{t - b}\\ 0 & 0 & 1 & -\frac{n+f}{n - f}\\ 0 & 0 & 0 & 1 \end{matrix}\right] =\left[\begin{matrix} \frac{2}{r-l} & 0 & 0 & -\frac{l+r}{r - l}\\ 0 & \frac{2}{t-b} & 0 & -\frac{t+b}{t - b}\\ 0 & 0 & \frac{2}{n-f} & -\frac{n+f}{n - f}\\ 0 & 0 & 0 & 1 \end{matrix}\right] \]
透视投影 Perspective Projection
被广泛应用的投影,原因是其成像与实际生活中得到的成像更为相似,有“近大远小”、“平行相交”的特性。
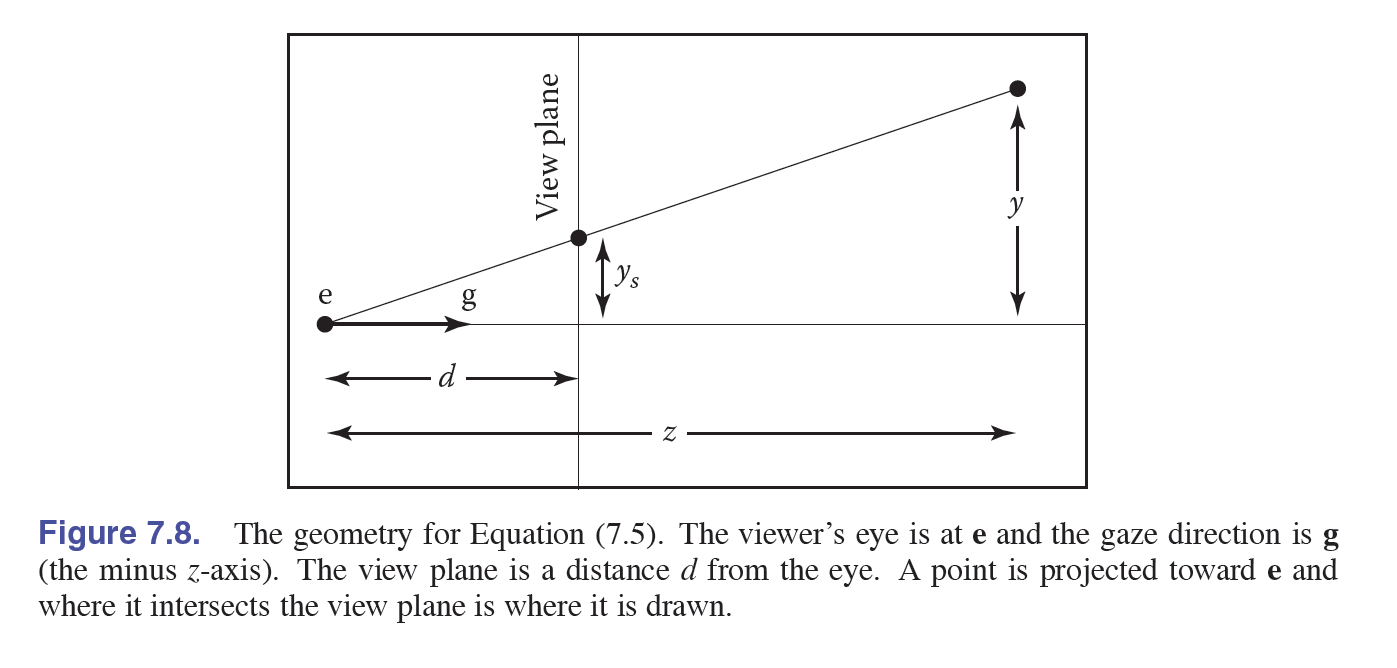
那么,如何得到一副透视投影?我们可以类比正交投影,发现:可以先将投影的三维梯形底面进行放缩至与目标投影面同样的大小, 再进行一次正交投影,则可以得到目标透视投影,
那么如何得到预处理矩阵\(M_{persp\rightarrow ortho}\)?根据上图,可以发现这是一个相似三角形,\(y_s:y = d:z\),于是有目标点为\((dx/z, dy/z, ?, 1)\), 将其乘上\(z\)得到\((dx, dy, ?, z)\),但是根据这些我们并不能知道原来的\(z\)变成了什么(因为放缩之后一方面\(z\)会发生变化,另一方面 \(z\)的目标位置并不是\(d\)(需要保持原有的先后顺序),于是我们便需要求出这个未知的值。
可以根据以下两条性质求出未知值:
- 在近平面的点\(z\)坐标不会改变
- 在远平面的点\(z\)坐标也不会改变
于是我们可以得到如下的转换矩阵
\[ M_{persp\rightarrow ortho} = \left[\begin{matrix} n & 0 & 0 & 0\\ 0 & n & 0 & 0\\ 0 & 0 & n+f & -nf\\ 0 & 0 & 1 & 0 \end{matrix}\right] \]
再将两个矩阵乘在一起,我们可以得到最终的变换矩阵
\[ M_{persp} = M_{ortho}M_{persp\rightarrow ortho} = \left[\begin{matrix} \frac{2n}{r-l} & 0 & \frac{l+r}{l-r} & 0\\ 0 & \frac{2n}{t-b} & \frac{b+t}{b-t} & 0\\ 0 & 0 & \frac{f+n}{n-f} & \frac{2fn}{f-n}\\ 0 & 0 & 1 & 0 \end{matrix}\right] \]
fov & aspect ratio
fov,全名 Field-of-View,代表眼睛的可视角度,在图形学里我们使用 fov 来代替直接使用 width x height 的表示方式,比如用\(fovY\)来表示 Y 轴方向的可视角度,这个时候我们可以通过投射面到摄像机的距离来得到对应的投射面宽高(其中\(aspectR=w/h\)),于是有
\[h = |n| \tan{fovY/2}\] \[w = aspectR \cdot h\]