“这游戏都是谁在赢？”：找到合适的竞技匹配模式

前言

经常玩英雄联盟红温的经常玩多人电子竞技游戏的人应该都知道一个游戏匹配机制的重要性。但是很多时候这些迭代多年，理论上应该相当成熟的系统，总是能给我们整个眼前一黑的好活，一局游戏下来完全无法确认你的队友的显示器前坐着的到底是不是智人。

在ACM SIGGRAPH Symposium on Interactive 3D Graphics and Games(I3D) 2024中则有一篇论文Skill-Based Matchmaking for Competitive Two-Player Games介绍了现有机制的缺陷和提出的一种全新匹配系统，笔者出于对队友智力的担忧匹配系统的兴趣，将从该论文出发，讨论现有匹配系统和评分机制。请注意，本文不是对原论文的翻译和直接总结。

什么比赛算好比赛

当然，在探讨优秀的匹配机制之前，我们应当定义比赛的精彩性。我们先以一对一的游戏为例（如国际象棋、格斗游戏和卡牌游戏等），排除那些抖S（喜欢虐菜的）和抖M（喜欢被高手虐的），大部分人喜欢的比赛应当是势均力敌的，这样的比赛一方面可以让我们享受到有来有回的竞技乐趣，另一方面通过适当的切磋总结也可以逐步提高我们的技术。

一个理想的系统应该总是为一位选手匹配到和其实力相近的对手，这首先要求系统可以对选手的实力进行量化，目前的游戏大多使用与选手账户对应的段位/排位分数\(r\)来衡量选手的这一指标。但是在游玩的过程中，选手的实力并不是一成不变的，系统需要逼近的理想分布为：

\[ r \sim s(t) \]

简单来说，系统最好在每场游戏结束后，给选手分数以恰当的变化量\(\Delta r\)来让\(r\)快速收敛，这就是一个理想的匹配系统应该具有的性质。显而易见的，如果存在这样的理想匹配系统，并且该系统中的选手数量足够多且选手实力满足类正态分布时，所有选手的胜率的期望值\(E[f_E] = 0.5\)，这应该通过以下两点实现，同时也是需要实际系统解决的两个问题：

1. 将选手的实力正确评估为分数，并且能让该分数随时间快速收。
2. 将分数相近的选手匹配到同一局游戏中。

How-to

对于单人竞技类游戏而言，问题2可以直接对单个选手的分数进行近似匹配解决，而有多个系统被提出以解决问题[1]。

“臭名昭著”的Elo Rating System

Arpad Elo在1978年出版的书籍The Rating of Chess Players Past and Present中首次提出了Elo系统（没想到吧，Elo其实是人名），这一系统因为被英雄联盟采用而广为人知，而对该系统谣传的误解通常如下：

Elo系统会给胜率高的人匹配胜率低的队友，来将所有人的胜率拉至接近50%的水准。

实际上，这一误解存在两点问题：

1. 所有人的胜率的期望值接近50%是任何竞技系统的最终目的，无关Elo或者其他系统。
2. Elo系统最初设计是用于国际象棋的评分，不涉及任何多人匹配的内容。

在这一点上达成共识后，我们就可以真正开始对初版Elo的介绍了。Elo致力于解决的是估计胜率和分数更新两个问题，首先考虑两个对战选手A、B的分数为\(r_A\)和\(r_B\)，那么在一场游戏中，A战胜B的概率为：

\[ f_E(A, B) = \frac{1}{1 + 10^{-(r_A - r_B) / 400}} \]

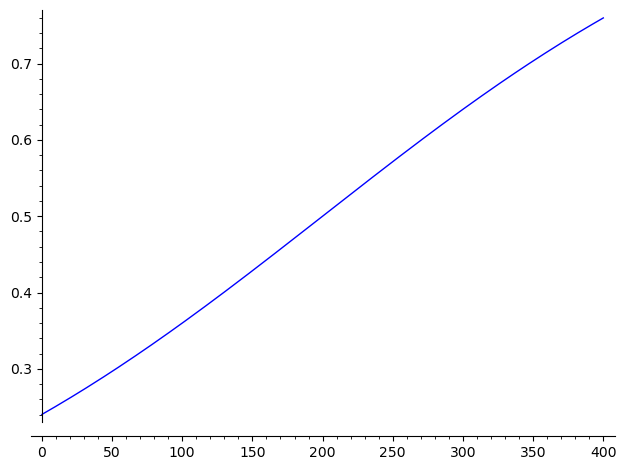👆在\(r_B = 200\)时，A的胜率随\(r_A\)的变化

该函数有两点优秀的性质：

1. \(f_E(A, B) + f_E(B, A) = 1\)，即该概率函数具有一致性。
2. 两者的胜率与自身分数的绝对值无关，仅与差值\(|r_A - r_B|\)和缩放系数\(400\)相关。

假设系统在\(m\)场比赛后，根据该系列赛的数据来更新选手的分数，具体的更新公式为：

\[ r'_A = r_A + K \sum_{i}^{m} \left( s_i - f_E(A, i) \right) \]

其中\(K\)是固定的分数更新常量，\(s_i\)代表比赛胜负带来的积分，赢、负、平分别为1、0和0.5分。这个更新的过程是符合直觉的：当一个选手在越没有可能战胜另外一个选手获胜时，得到的分数越多，当已经是在虐菜时，则几乎不得分。该过程类似于梯度下降，通过一个batch的学习来更新参数。

但是Elo初始方法的缺点也很明显：

1. 胜率和分数均通过一个常数400（可更改）控制，如何合理地给与选手初始分数值得商榷。
2. 分数更新的系数\(K\)固定，并且不随游戏过程发生变化，如何选择一个合适的值使其在一名选手的前期不至于收敛过慢、后期不至于导致变化过于剧烈无法衡量。
3. 该系统没有考虑选手对于对战的偏好性，若出现类似于环状的关系：A选手的风格正好压制B，而B压制C，C压制A，系统则难以收敛。
4. 该系统基于部分群体（与A比赛的人）来衡量A的实力，没有考虑整个选手群体的情况。

Glicko Rating Systems

Glickman在1999年提出了Glicko rating system，该系统在Elo的胜率估计和分数更新上加入了额外的评分误差函数\(g(\phi)\)来让系统更容易收敛，具体的公式就不贴了。简单来说Glicko系统通过引入更复杂的\(g(\phi)\)和\(K_G\)来让选手的分数后期更具有收敛稳定性，减少了需要人为选择的常量。

但是该系统仍然未能解决Elo系统存在的问题[3]和[4]，并且新的胜率函数\(f_G\)不具有一致性（和非1）。

多人游戏中的Elo

TBC，如果有人看的话。。。