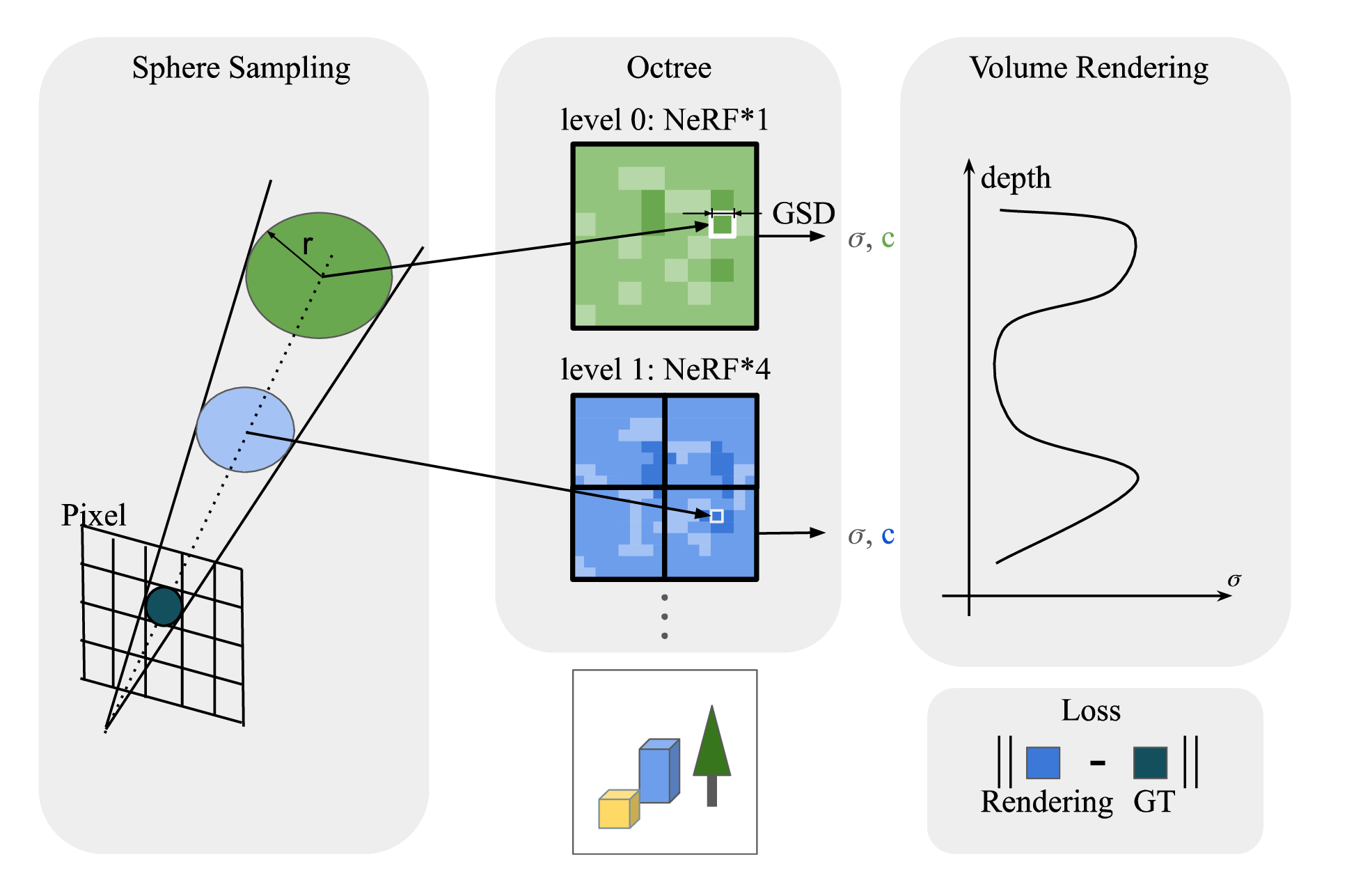
InfNeRF: Towards Infinite Scale NeRF Rendering with O(log n) Space Complexity
用八叉树给 NeRF +NGP 叠上了八叉树,每个八叉树节点再用 2048 的 NGP Nerf,不懂 NeRF,但是看起来像 A+B 的工作

GS^3: Efficient Relighting with Triple Gaussian Splatting

InfNeRF: Towards Infinite Scale NeRF Rendering with O(log n) Space Complexity
用八叉树给 NeRF +NGP 叠上了八叉树,每个八叉树节点再用 2048 的 NGP Nerf,不懂 NeRF,但是看起来像 A+B 的工作

GS^3: Efficient Relighting with Triple Gaussian Splatting
fiber 纤维,股的组成部分 ply 股(织线的组成) yarn 纺线,n-ply yarn,n股纺线 - ply level 由ply不同的数量、缠绕的方式造成的yarn的不同外观 woven cloth 梭织 - warp-weft 经-纬 knitted cloth 针织 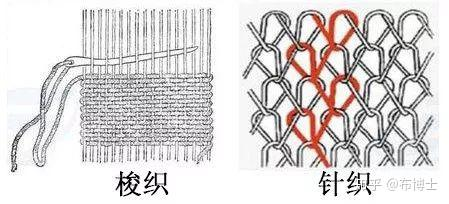 - knittet coth 会由于缠绕方式的不同产生体积/阴影遮挡效果,这个层级被称为pattern level
- knittet coth 会由于缠绕方式的不同产生体积/阴影遮挡效果,这个层级被称为pattern level
PBR论文简读:Better BSSRDF Models(1)
在上一篇简读论文:PBR论文简读:A Practical Model for Subsurface Light Transport(后文将以Basic BSSRDF模型来指代本文提出的模型)提出BSSRDF模型后,人们陆陆续续发现了模型中的很多不足与需要改进的地方,因此接下来几篇blog将会简读几篇关于Basic BSSRDF模型的改进方法相关的论文。
这篇论文主要指出了Basic BSSRDF中没有考虑到薄介质、多层、粗糙接触面的非理想情形下的问题,提出了多层(Multi-Layered)的BSSRDF模型。
PBR论文简读:A Practical Model for Subsurface Light Transport
离线环境下进行真实感渲染的时候,会有各种散射材质,比如人类皮肤、硅胶等。从外观上看,这类材质的通性在于都有一种“透光”的感觉,简单的使用brdf创造出来的材质往往显得很生硬,因此Jensen'01的这篇论文给出了一个实际的次表面散射(subsurface scattering)bxdf来实现这种材质。
BRDF理论假设材质光的进入和离开的起、终点一致,本质上是对BSSRDF的一种近似\(x_o = x_i\),并且给出的积分公式也是简单地在半球面上进行积分,BSSRDF则考虑的是出、入射点不同时,对于区域\(A\)内所有入射光线的radiance的半球面积分:
\[L_o = \int_A\int_{2\pi}S\cdot L_i\cdot (\vec n\cdot \vec {\omega_i})d\omega_i dA(x_i)\]
对图像的描绘,本质上是场景重建(reconstruction)与信号处理(signal processing),简单来说就是用离散的采样(像素点)来对连续的真实世界进行重建,那么就涉及到采样(sampling)的问题了。
傅立叶分析可以用来评估重建函数的质量,同时其被用来在频域上分析不同频率的函数,通常来说,高频率的函数变换的较为频繁、较快;低频率的函数变化的较缓慢。如下是两个函数图像:
与之对应的,是其在频域上的函数图像:
众所周知,自然、物理界的光照不是靠RGB三个离散分量描述的,而是由不同强度的不同波长\(\lambda\)的光组成的,因此如果要基于物理地渲染,对于自然光谱的模拟是必不可少的,在pbrt和mistuba两款渲染器中,都采用了Spectrum类来承载光谱数据,对于不同波长的数据,我们描述为SPD,aka spectral power distribution,光谱能量分布。
自然界光谱不是离散描述的,于是我们可以像傅立叶变换一样,用一组带系数的基底函数\(c_iB_i(\lambda)\)来逼近实际的波形。
pbrt中,定义了两种实际的Spectrum类,并且使用一个typedef来在实际的使用中切换两者的类型:
1 | typedef RGBSpectrum Spectrum; |
在整个图形学领域,空间中的物体都是由基本的Shape构成的,比如基本的几何形体:Sphere、Box;或者能够达成更加复杂表现的Mesh等。这一章主要讲述了几种不同的形体的定义和相关计算。
PBRT使用Shape类来为所有形体创建了一个基类,reverseOrientation用来决定图形的法线是否翻转(用来确定图形的内、外)。
对于每个形体有如下的基础函数和解释:
1 | virtual Bounds3f ObjectBound() const = 0; |
PBR论文实现:Marschner's/d'Eon Hair Model
在完成GAMES101大作业的时候,选择了Marchner的毛发模型的实现,先后参考了两篇论文,总算是做出来像个东西了。
我阅读的第一篇论文是《Light Scattering from Human Hair Fibers》,这篇文章属于是现在的毛发渲染的开山鼻祖了。
这篇论文开创性地提出了毛发的表皮含芯的模型:
作者认为人类的毛发不是单纯的一个柱状模型(Kajiya模型),而是表皮(cuticle)加上柱芯(cortex)的组合。同时,将毛发的不同颜色归因于柱芯对于不同波长光的吸收率不同,从而导致毛发出现不同的颜色。很重要的,这个模型将光线从单纯的反射(brdf)拓展为了多个不同的类别(bcsdf),其中Marschner的这篇论文着重强调了其中的三个组成项:R、TT、RTR,R代表一次反射(reflection),T代表一次在柱芯中的传播(transmission),这里我们也可以得到,R项是没有受到吸收的,所以R项应该是造成高光的项。
PBR读书笔记一:Geometry & Transformation
这会是一个持续更新的系列,用来记录我在阅读《Physically Based Rendering》的一些读书心得和brief。
之前玩Unity的时候就有过使用四元数的经历,当时还不太明白万向锁和四元数的本质,看了这一章之后遍会有更加深入的体会。
四元数发明的初衷是对于复数的拓展,\(q=(x,y,z,w)=w+x\vec i+y\vec j+z\vec k\),ijk四个量的乘法运算是非交换的。与此同时,\(q=(q_{xyz}, w)\),因此对两个四元数做点乘,两个分量:
\[(q\cdot q')_{xyz} = q_{xyz}\times q'_{xyz} + q_wq'_{xyz} + q'_wq_{xyz}\]