从物体空间到屏幕:深入理解变换矩阵
前言
最近在学习写一个离线渲染器的时候,有一个需求是要实时地追踪一条射线逐个打到的物体然后显示debug信息的功能(顺便一说,这个功能真的很好用也很好玩),离线部分仿照的pbrt-v3,交互的前端则是使用的imgui+OpenGL。前面的实现都很顺利,但是到渲染车辆场景的时候,发现射线没有做到指哪打哪,那肯定是出问题了,于是我从头到尾地排查了一遍所有的变换相关的代码。发现了两个问题:
- OpenGL中裁剪空间的Z轴范围要求范围为\([-1, 1]\),而pbrt的
perspective矩阵变换的Z范围为\([0, 1]\)。 - OpenGL需要在NDC之前就考虑viewport的长宽比aspect,但是pbrt将这一步推迟至了cameraToRaster。
进行排查的同时也系统化地解决了大量疑问:
- 老生常谈的
MVP矩阵到底是在哪些空间中进行变换? - 变换的结果范围是什么?
- 用的是左手还是右手坐标系?
- ...
作为一个总结,这篇博文会对图形学中的矩阵变换进行一次统一的梳理以加深理解,并且能够成功解答这些疑问。
左手系vs右手系
要定义一套坐标系统,一个前提就是确定坐标系的三个基单位向量,这三个向量必然是线性无关并且两两正交的。当确定了其中的两个向量(x、y)后第三个向量的确定就有两个方向可以选择了,这两个方向是正好相反的,因此就诞生了有了左手系和右手系的区别。
确定左右手系的方法如其名,用大拇指代表x向量,用食指代表y向量,分别指向右侧和上方,然后剩下的中指就是z向量,这三个向量两两正交,因此左右手会自然呈现出两种不同的形态:
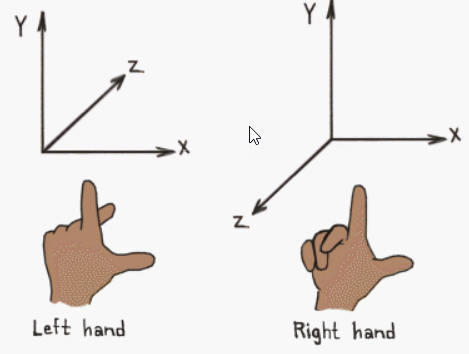
叉乘?
需要注意的是,在这两种坐标系下,叉乘的定义都是不变的,即对于\(\vec v_1 = (x_1, y_1, z_1)\)和\(\vec v_2 = (x_2, y_2, z_2)\),有:
\[ \vec v_1 \times \vec v_2 = (y_1z_2 - z_1y_2, z_1x_2 - x_1z_2, x_1y_2 - y_1x_2) \]
谁在用这些坐标系?
在一般生活中,我常见到的坐标画法是右手系,但是图形学的应用中两种手系均有人使用,比如pbrt使用的就是左手系。一个常见的谬误就是可编程管线中OpenGL或者DirectX使用了某一个特定的坐标系。实际上,只有固定功能管线才会使用固定的坐标系,如OpenGL2.0以前的版本使用的是右手系,而DX9默认使用的是左手系(可更改);而在可编程管线中,管线在顶点着色器之后经过固定的透视除法得到的NDC坐标就已经和左/右系无关了,NDC中的z轴范围为\([-1, 1]\),越小离相机越近,越大离相机越远,这个定义是固定的,和左右手系完全无关。
但是用户在进行VP坐标变换的时候则必须自己考虑坐标系的问题,这个问题会在接下来的内容中详细讨论。
从物体空间到世界空间
用过Unity的人应该对ObjectToWorld这个矩阵很熟悉,通常这个矩阵被用在有层级的物体上。这样就可以将子物体的坐标系变换到父物体的坐标系中,再由父物体变换到世界坐标系中,这样就可以得到子物体在世界坐标系中的坐标了。
这也就是MVP中的M,模型矩阵。
从世界空间到相机空间
接下来,我们需要从相机的方向观察世界坐标中的所有点,为了简化操作,这一步的具体过程就是假设将相机放置于原点\((0, 0, 0)\),然后沿着z轴观察世界。我们需要做的就是找出这个相机的坐标系,然后将所有的点变换到这个坐标系中,这一步中常用的方法是被称为lookat的矩阵,具体组成如下:
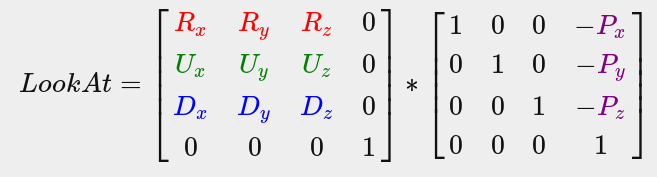
需要求的几个向量分别是Right(x)、Up(y)、Direction(z)和Position,已知Position、Direction是确定的(前者是相机位置,后者是需要给定的参数),使用用户传入的\(U'\)确定一个平面来构建Right,接下来的工作就是求出\(R\)和\(U\)两个向量。
那么问题就来了,我知道\(R\)向量是由\(U'\)和\(D\)叉乘得到的,那么叉乘的顺序应该是什么呢?这里就涉及到了坐标系的手性问题了。在左手系中,我们将相机放置在原点,并且使其看向\(z\)轴正方向;右手系则反之,使其看向\(z\)轴负方向。 让我们看看glm中的左、右手系是怎么求这三个向量的:
1 | template<typename T, qualifier Q> |
对于右手系,\(R = D \times U'\),
从物体空间到屏幕:深入理解变换矩阵