程序化生成：Perlin噪声和Simplex噪声

首先摘抄一段wiki上对于Perlin噪声的介绍：

Perlin噪声（Perlin noise）指由Ken Perlin发明的自然噪声生成算法。由于Perlin本人的失误，Perlin噪声这个名词现在被同时用于指代两种有一定联系的的噪声生成算法。这两种算法都广泛地应用于计算机图形学，因此人们对这两种算法的称呼存在一定误解。下文中的Simplex噪声和分形噪声都曾在严肃学术论文中被单独的称作Perlin噪声。

接下来，我将围绕生成一张2D噪声纹理为目标展开对于几种噪声生成方法的介绍。

Why

为什么我们需要这两种新的噪声生成方法？对于噪声的生成方法，最为平凡的办法当然是对于每个点取一个均匀分布的随机数，如，生成一个\([0,1]\)的uniform随机数，然后直接将其作为灰度值使用：

使用随机方法产生的白噪声，来自wiki

嗯，很符合我们对于噪声的想象，但是是不是缺了点什么？观察自然中的很多东西，比如山脉地形、云体等，我们可以将其高度、密度等分布视作是完全随机的，但是和上面的白噪声是有很大区别的，很明显的一个区别就是白噪声不够连续。Perlin指出，一个理想的噪声应该拥有以下的特征：

• 对旋转具有统计不变性；
• 能量在频谱上集中于一个窄带，即：图像是连续的，高频分量受限；
• 对变换具有统计不变性。

虽然在统计学上可能不比白噪声“随机”，但是这样的噪声很明显是更加真实且实用的。对于连续性，我们很容易想到对近邻进行采样的方法来实现，但是这是相当低效的：对近邻采样就意味着过程需要是串行执行的，对于图形学这种需要运行在GPU上的应用相当不友好，因此Perlin噪声便是我们的第一个选择。

Perlin噪声

Perlin噪声是以空间中的晶格为单位进行生成的，简单来说就是把空间划分为等长度/面积/体积的区块，然后针对每个区块进行运算：对于1D空间，晶格对x轴进行等宽的划分；对于2D空间，晶格将空间划分为一个个矩形；对于3D空间或者更高维的空间，则是（超）立方体。

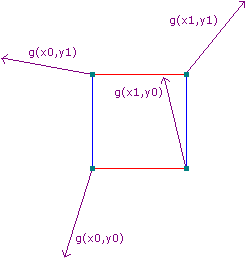
接下来，对于每个晶格的顶点，我们随机分配一个梯度 gradient（如上图），梯度是一个向量，一维情况下则是一个斜率，相邻的晶格共享顶点的同时也会共享梯度。然后对于晶格里面的任意一个采样点，我们可以计算出晶格的各个顶点指向这个uv坐标的\(\delta\)向量，对于2D的情况来说，就是矩形的四个顶点指向采样点的四个向量：

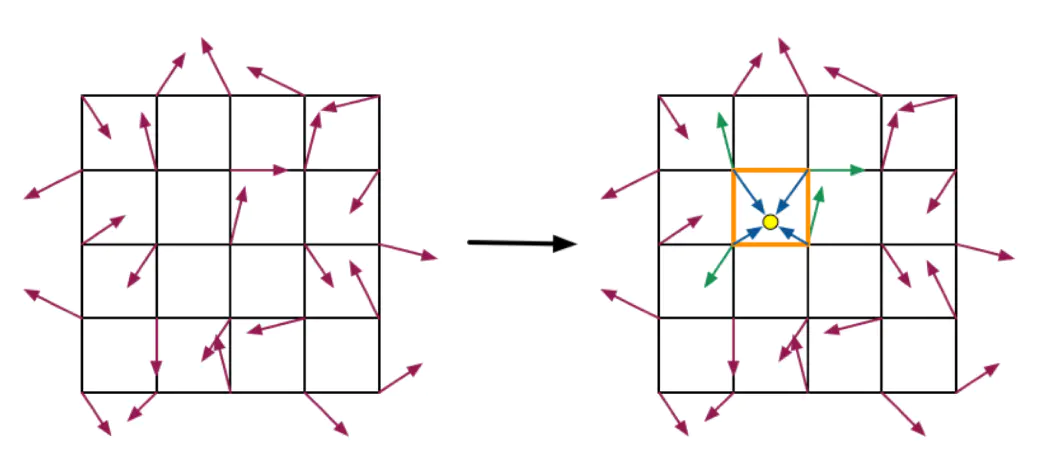
我们将每个顶点对应的delta向量和gradient向量点乘，得到采样点在四个顶点的噪声值，接下来就很简单了，用二维插值的方法，根据uv坐标计算出采样点的噪声值：

但是——等等，好像看起来不太对！每个晶格之间有很明显的分割痕迹，这是为什么？原因很简单，我们这里使用了线性的插值函数：

\[lerp(a, b, t) = a (1 - t) + bt\]

这样的结果就是晶格与晶格之间的过渡不够平滑（很符合直觉），因此我们可以使用一个平滑过度的高次函数，Perlin在其最初的论文中提出的函数不够优秀，最终选用的函数为\(6t^5 - 15t^4+10t^3\)

Perlin噪声的实现

这里我们选用了Taichi语言来实现柏林噪声，总结一下上面的流程，步骤如下：

1. 将空间划分为等大小晶格
2. 对于晶格的顶点分配梯度，共享的顶点在不同晶格之间共享相同的梯度
3. 计算采样点相对晶格的位置，计算出delta向量
4. 对应计算出顶点梯度和delta向量的点积结果
5. 对点积结果根据采样点在晶格中的uv位置进行非线性插值，得到采样点的噪声值

首先我们定义图片大小为512x512，规定晶格大小为64，这样就把平面划分为了8x8的晶格：

window_size = (512, 512)
pixels = ti.field(ti.f32)
hl = ti.root.dense(ti.i, window_size[0]).dense(ti.j, window_size[1])
gs = 64.0
hl.place(pixels)

接下来，对于每个采样点，我们接收整数x, y作为坐标，计算出在晶格空间中的坐标\([0, 8]\times[0,8]\)：

u = (x + z) / gs
v = (y + z) / gs
# 晶格边界
u0 = ti.floor(u, ti.i32)
v0 = ti.floor(v, ti.i32)
u1 = u0 + 1
v1 = v0 + 1

接下来，我们需要针对晶格找到其对应的梯度，我们认为，对于二维的梯度，使用8个预分配的梯度值，然后每次随机地从这8个梯度值中取出一个即可，很明显如果顺序的反复取用很容易造成重复导致的人工痕迹，因此Perlin提出使用一个额外的转置数组 Permutation Array来伪随机地对于这几个梯度进行取用，只要转置数组打乱地足够好，那么就可以认为得到地梯度是近似于随机的。

ptable = ti.field(ti.i32, shape=512)
ptable.from_numpy(np.array([151, 160, 137, 91, 90, 15, 131, 13, 201, 95, 96, 53, 194, 233, 7,
                            225, 140, 36, 103, 30, 69, 142, 8, 99, 37, 240, 21, 10, 23, 190, 6, 148, 247,
                            120, 234, 75, 0, 26, 197, 62, 94, 252, 219, 203, 117, 35, 11, 32, 57, 177, 33,
                            88, 237, 149, 56, 87, 174, 20, 125, 136, 171, 168, 68, 175, 74, 165, 71, 134,
                            139, 48, 27, 166, 77, 146, 158, 231, 83, 111, 229, 122, 60, 211, 133, 230, 220,
                            105, 92, 41, 55, 46, 245, 40, 244, 102, 143, 54, 65, 25, 63, 161, 1, 216, 80,
                            73, 209, 76, 132, 187, 208, 89, 18, 169, 200, 196, 135, 130, 116, 188, 159, 86,
                            164, 100, 109, 198, 173, 186, 3, 64, 52, 217, 226, 250, 124, 123, 5, 202, 38,
                            147, 118, 126, 255, 82, 85, 212, 207, 206, 59, 227, 47, 16, 58, 17, 182, 189,
                            28, 42, 223, 183, 170, 213, 119, 248, 152, 2, 44, 154, 163, 70, 221, 153, 101,
                            155, 167, 43, 172, 9, 129, 22, 39, 253, 19, 98, 108, 110, 79, 113, 224, 232,
                            178, 185, 112, 104, 218, 246, 97, 228, 251, 34, 242, 193, 238, 210, 144, 12,
                            191, 179, 162, 241, 81, 51, 145, 235, 249, 14, 239, 107, 49, 192, 214, 31, 181,
                            199, 106, 157, 184, 84, 204, 176, 115, 121, 50, 45, 127, 4, 150, 254, 138, 236,
                            205, 93, 222, 114, 67, 29, 24, 72, 243, 141, 128, 195, 78, 66, 215, 61, 156, 180] * 2))

grad_table = ti.Vector.field(2, ti.f32, shape=8)
grad_table.from_numpy(np.array([(1, 2), (2, 1), (-1, 2), (-2, 1), (-1, -2), (-2, -1), (1, -2), (2, -1)]))

@ti.func
def grad(U, V):
    s = ptable[(ptable[U & 255] + V) & 255]
    return grad_table[s & 7]

grad函数接收两个整数作为随机种子，通过两次在转置数组中取值来得到梯度值，而我们需要每个晶格的顶点梯度保持一致，那么理所当然的输入的两个随机种子就是晶格顶点坐标，接下来就是把两个变量点乘得到结果，对四个点乘结果进行二维插值即可得到结果：

@ti.func
def dot_prod(u, v, ug, vg):
    delta = ti.Vector([u - ug, v - vg])
    grad = grad(ug, vg).normalized()
    return ti.math.dot(delta, grad)

@ti.func
def perlin_noise(x, y, z):
    ...
    prod00 = dot_prod(u, v, u0, v0)
    prod01 = dot_prod(u, v, u1, v0)
    prod10 = dot_prod(u, v, u0, v1)
    prod11 = dot_prod(u, v, u1, v1)
    result = lerp2D(prod00, prod01, prod10, prod11, u - u0, v - v0)

最后，完整、可运行的代码如下：

import taichi as ti
import numpy as np
from time import time
ti.init(arch=ti.cuda, debug=True)

window_size = (512, 512)

pixels = ti.field(ti.f32)
# hierarchical layout
hl = ti.root.dense(ti.i, window_size[0]).dense(ti.j, window_size[1])
# flat layout
# fl = ti.root.dense(ti.i, 400).dense(ti.j, 400)
gs = 64.0
hl.place(pixels)

# len = 256
ptable = ti.field(ti.i32, shape=512)
ptable.from_numpy(np.array([151, 160, 137, 91, 90, 15, 131, 13, 201, 95, 96, 53, 194, 233, 7,
                            225, 140, 36, 103, 30, 69, 142, 8, 99, 37, 240, 21, 10, 23, 190, 6, 148, 247,
                            120, 234, 75, 0, 26, 197, 62, 94, 252, 219, 203, 117, 35, 11, 32, 57, 177, 33,
                            88, 237, 149, 56, 87, 174, 20, 125, 136, 171, 168, 68, 175, 74, 165, 71, 134,
                            139, 48, 27, 166, 77, 146, 158, 231, 83, 111, 229, 122, 60, 211, 133, 230, 220,
                            105, 92, 41, 55, 46, 245, 40, 244, 102, 143, 54, 65, 25, 63, 161, 1, 216, 80,
                            73, 209, 76, 132, 187, 208, 89, 18, 169, 200, 196, 135, 130, 116, 188, 159, 86,
                            164, 100, 109, 198, 173, 186, 3, 64, 52, 217, 226, 250, 124, 123, 5, 202, 38,
                            147, 118, 126, 255, 82, 85, 212, 207, 206, 59, 227, 47, 16, 58, 17, 182, 189,
                            28, 42, 223, 183, 170, 213, 119, 248, 152, 2, 44, 154, 163, 70, 221, 153, 101,
                            155, 167, 43, 172, 9, 129, 22, 39, 253, 19, 98, 108, 110, 79, 113, 224, 232,
                            178, 185, 112, 104, 218, 246, 97, 228, 251, 34, 242, 193, 238, 210, 144, 12,
                            191, 179, 162, 241, 81, 51, 145, 235, 249, 14, 239, 107, 49, 192, 214, 31, 181,
                            199, 106, 157, 184, 84, 204, 176, 115, 121, 50, 45, 127, 4, 150, 254, 138, 236,
                            205, 93, 222, 114, 67, 29, 24, 72, 243, 141, 128, 195, 78, 66, 215, 61, 156, 180] * 2))

grad_table = ti.Vector.field(2, ti.f32, shape=8)
grad_table.from_numpy(np.array([(1, 2), (2, 1), (-1, 2), (-2, 1), (-1, -2), (-2, -1), (1, -2), (2, -1)]))
minn = ti.field(ti.f32, shape=())


@ti.func
def smooth(t):
    return 6.0 * ti.pow(t, 5.0) - 15.0 * ti.pow(t, 4.0) + 10.0 * ti.pow(t, 3.0)


@ti.func
def lerp(v1, v2, t):
    g = 1.0 - smooth(t)
    return v1 * g + v2 * (1.0 - g)


@ti.func
def lerp2D(v00, v01, v10, v11, tu, tv):
    v0y = lerp(v00, v01, tu)
    v1y = lerp(v10, v11, tu)
    return lerp(v0y, v1y, tv)


@ti.func
def grad(U, V):
    s = ptable[(ptable[U & 255] + V) & 255]
    return grad_table[s & 7]


@ti.func
def dot_prod(u, v, ug, vg):
    delta = ti.Vector([u - ug, v - vg])
    grad = grad(ug, vg).normalized()
    return ti.math.dot(delta, grad)


@ti.func
def perlin_noise(x, y, z):
    u = (x + z) / gs
    v = (y + z) / gs
    u0 = ti.floor(u, ti.i32)
    v0 = ti.floor(v, ti.i32)
    u1 = u0 + 1
    v1 = v0 + 1

    prod00 = dot_prod(u, v, u0, v0)
    prod01 = dot_prod(u, v, u1, v0)
    prod10 = dot_prod(u, v, u0, v1)
    prod11 = dot_prod(u, v, u1, v1)

    result = lerp2D(prod00, prod01, prod10, prod11, u - u0, v - v0)
    return (result + 0.707) / 1.414


@ti.kernel
def render(t: ti.f32):
    for x, y in pixels:
        pixels[x, y] = perlin_noise(x, y, t)


if __name__ == '__main__':
    window = ti.ui.Window('Perlin Noise', window_size)
    canvas = window.get_canvas()
    t = 0.0
    last_time = float(time())
    while window.running:
        now_time = float(time())
        delta_time = now_time - last_time
        t += delta_time
        last_time = now_time
        render(t * 100.0)
        canvas.set_image(pixels)
        window.show()

比较有趣的是，这样计算出来的Perlin并不是落在一个标准的范围中，我只是简单地认为其落在\([-\sqrt{2} / 2, \sqrt{2} / 2]\)的范围中，关于这个问题可以参考stackoverflow上的这个回答。实现的效果图如下：

很简单地，我们可以将Perlin噪声拓展到3D空间，并且将时间\(t\)作为第三维输入，这样就可以得到在空间中平滑变换的Perlin噪声。

Simplex噪声