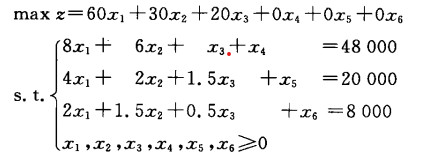运筹学期末复习
可作为复习资料打印
线性规划问题的单纯形法
线性规划的标准模型,下面给出一个例子
\[\max z = c_1x_1+c_2x_2+c_3x_3+c_4x_4\]
\[ \left\{\begin{array}{lr} a_{11}x_1+a_{12}x_2+a_{13}x_3+a_{14}x_4=b_1 &\\ a_{21}x_1+a_{22}x_2+a_{23}x_3+a_{24}x_4=b_2 &\\ a_{31}x_1+a_{32}x_2+a_{33}x_3+a_{34}x_4=b_3 &\\ a_{41}x_1+a_{42}x_2+a_{33}x_3+a_{44}x_4=b_4 &\\ x_1,x_2,x_3,x_4\ge 0 \end{array} \right. \]
- \(\vec b\) 需要满足 \(\vec b \ge 0\)
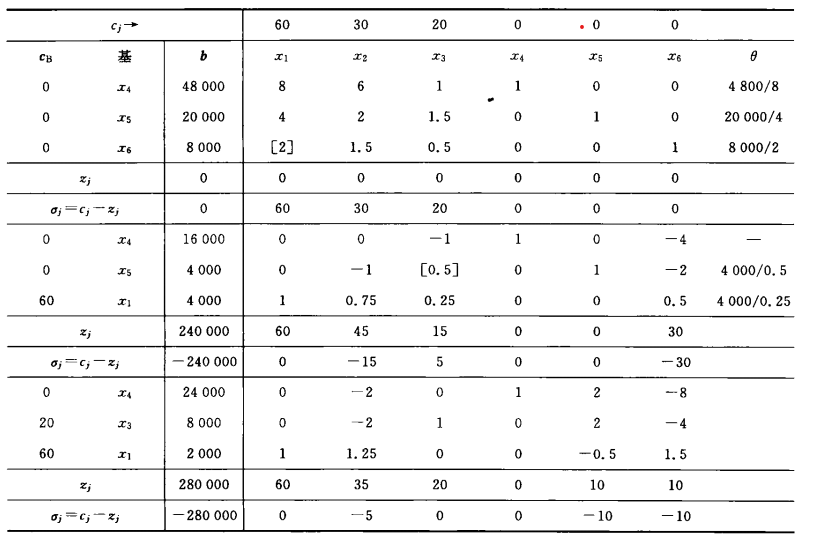
单纯形法
对于一个线性规划问题如
可以作出以下的单纯形表
单纯形表求解步骤
- 对原问题进行标准化
- 找到一个初始可行基\(\bar B\)(即对应的系数矩阵为一个单位矩阵)
- 求出此时每列变量\(x_i\)对应的 \(z_j = \sum c_Ba_{ij}\),\(\sigma_j=c_j-z_j\)
- 当\(\exist \sigma_j > 0\)时,说明不是最优解,继续进入第四步,反之结束迭代,进入步骤
8. - 选出\(\max\sigma_j\),选定该列对应的变量为换入变量
- 对于每一行,求得 \(\theta=b_j/\max{a_{ij}}\),其中要求\(a_{ij}>0\) 且 对应的列不能是基中的。选出\(\min\theta\)对应的一行的变量为换出变量
- 用高斯消元法,将对应的换入变量(方括号括中的)化为 1,对应列其余系数化为 0,得到新的表。
- 返回
步骤2. - 最终解为表左边的基变量,对应的基变量的值为右方的\(b\)
有最优解 非基变量\(\sigma_j\le 0\),基变量 \(\sigma_j=0\)
唯一最优解 有最优解的情况下,所有非基变量的 \(\sigma_j<0\)
无穷多最优解 有最优解的情况下,存在非基变量的 \(\sigma_j=0\)
无最优解 所有的系数 \(a_{i,m+k}\le 0\),且仍有一个非基变量的 \(\sigma_j>0\)
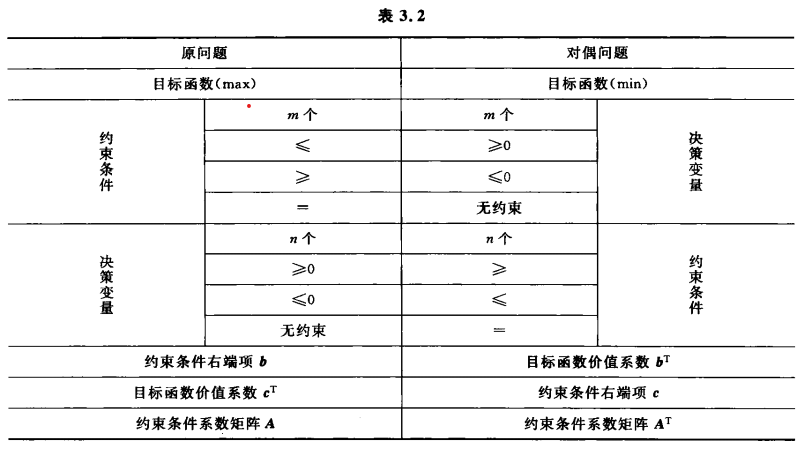
线性规划的对偶 P65
若原问题为
\[\max\vec{c}^T\vec x\]
\[ \left\{\begin{array}{lr} \vec A \vec x\le \vec b &\\ \vec x \ge 0 \end{array}\right. \]
则其对应的对偶问题为
\[\min\vec{b}^T\vec y\]
\[ \left\{\begin{array}{lr} \vec A^T \vec y\ge \vec c &\\ \vec y \ge 0 \end{array}\right. \]
可以得出:原问题的每个不等式对应对偶问题中的一个变量,其具体关系如下表
对偶定理 P68
对于一个问题及其对偶问题,有:
弱对偶定理 原问题的任意可行解的目标函数值是对偶问题的目标函数值的下界;反之,对偶问题的目标函数值为原问题的目标函数的上界
- 即 max 为 min 的下界,min 为 max 的上界
最优解存在性定理 若原问题和对偶问题均存在可行解,则它们必定存在最优解
无界解定理 若两个问题的都有可行解,且其中一个目标函数无界,则其另一个无可行解
强对偶定理 若其中一个有最优解,则另一个也有,且目标函数的值相等
互补松弛定理(P71) 将问题化为标准形式,将最优解\(\vec x^*\)带入标准型中,求得松弛变量取值,再利用两个等式
\[\vec y^*\vec x_S = 0\]
\[\vec y_S\vec x^* = 0\]
将求出的值代入对偶问题的标准型,再求出剩下的变量的值。
对偶单纯形法(P75) 对于标准形式的线性规划问题(\(b\)可小于等于 0),若\(b\)中不存在负数,则跳出;反之选择其中绝对值最大的,对应行为出基变量,计算\(\sigma_j/a_{ij}, a_{ij}<0\wedge \sigma_j<0\)(如果所有\(a_{ij}>0\),则对偶问题没有可行解)比值最小的列对应变量为入基变量。
灵敏度分析 P79
资源系数 \(\vec b\) 变化 P80
\(\vec x = B^{-1}(b+\Delta b)\ge 0\)时,原最优解不变,其中\(B^{-1}\) 为原基变量的系数矩阵
已知资源系数的改变量\(\Delta b\) 直接用上式求出新的\(b\),用对偶单纯形法继续迭代。
价值系数 \(\vec c\) 发生变化 P81
非基变量 若要原解不变,只需要对应系数\(c_j\)使得\(\sigma_j\le0\)即可保持原最优解不变。
基变量 需要保证所有非基变量的检验数\(\sigma_j\le 0\)。
如果题中有指出已经发生了变化,将变化的系数带入单纯形表中继续迭代即可。
技术系数 \(A\) 发生变化 P83
非基变量 对于该技术系数对应的列,左乘上一个\(C_B\)和原基变量的最终形表矩阵\(B^{-1}\),即\(c_BB^{-1}\),保证对应的\(\sigma_j\le 0\)即可保持原最优解不变。
基变量 见下表以及 P84 的详细讲解。
运输问题 P92
表上作业法(P96)
表的每个格中,单位运费写在左上角,右下角若为基变量则写\(x_{ij}\)即调用的数目,若为非基变量则写\([\sigma_{ij}]\)(对应格的检验数)。
初始基可行解确定(最小元素法 P99) 每次选择费用最小的一个格,根据供应量在需求量减去对应的最大值,如果需求量减后为 0,则划去这列;如果对应的供应量减后为 0,则划去这列,反复迭代直到所有的需求都被满足。
检验最优性(闭回路法) P105 从一个非基变量格出发,画一个闭回路,要求回路上的其余所有顶点均为基变量,再将各个顶点从起点为 0 开始编号,对应非基变量的检验数\(\sigma = 偶数点运价和-奇数点运价和\),若所有检验数大于等于零,则对应的方案为最优方案。
- 无穷多最优解:非基变量检验数为 0
- 退化问题
- 找基可行解时,导致列和行同时饱和,同时划去这一行和这一列,除了交叉的点以外其余\(x\)取 0,导致得到了退化的基可行解
- 闭回路法调整时,有多个最小奇数顶点,只能取一个为换出变量,则得到了一个\(x_{ij}=0\)的退化解
方案调整 P109
- 选取负检验数中的最小者,作为换入变量
- 找闭回路并且编号,方法同上
- 找出奇数编号顶点中\(x\)最小的,作为调整量\(\theta\),作为换出变量
- 将回路中所有奇数点减去\(\theta\),偶数点加上\(\theta\),获得新的可行解
- 继续检验调整
指派问题 P129
已知每个人只能做一个工作,并且已知所有人做某个工作的费用,得到费用矩阵\(C\),需要求使得费用最小(\(\min z\))的解零一矩阵
匈牙利算法 P132
对于给定费用矩阵 \(C,\quad(n=r(C))\) 的指派问题
- 将费用矩阵\(C\)每行每列分别减去其对应行/列中的最小元素值得到\(C'\)
- 先逐行检验,若一行中只有一个未标记过或者只有一个没被叉标记的 0 元素,则将其括起,将其所在列的其他未标记 0 元素用叉
X划去。重复进行直至每一行都没有被 0 标记或者有 2 个以上没有被标记的 0 - 列检验,同理 2.
- 将括了的(0)元素对应的解矩阵\(X\)中的元素置 1,其余元素置 0
步骤3结束后有可能会有如下几种情况 P133
- 每一行都有被括的 0,个数\(m=n\)
- 跳入步骤
4
- 跳入步骤
- 存在未被标记的零元素,但是其对应的行或者列中未被标记过的零元素都至少有两个
- 选择 0 元素少的行/列的某个 0 加括号
- 用叉划去其他 0 元素,再进行行、列检验
- 所有 0 均被标记,但是数量小于\(n\)
P134(此处略过)
其他指派问题
最大化指派问题 P136 即需要求\(\max z\),可用矩阵中的最大元素减去矩阵中每个元素得到新矩阵,再使用匈牙利算法求解。
人数和事件数不等 P137 增加费用为 0 的人/事件,使用匈牙利算法求解
一个人可以同时做多件事 P138 将这个人的费用行复制一遍,再将人数和事件数调整至一致,使用匈牙利算法,求解得到的解矩阵为对应人需要做的多件事。
某事不能由某人去做 将这个人做这件事的费用取为一个足够大的 M
博弈论
两人有限零和博弈
游戏中有两个博弈者,每人均有有限个博弈策略可选,且两人的得失综合恒为 0。
博弈者分别有各自的策略集 \(S_\alpha=\{\alpha_1,\alpha_2,...,\alpha_n\}\) 和 \(S_\beta=\{\beta_1,\beta_2,...,\beta_m\}\),则有博弈者的支付矩阵
\[ A=\begin{bmatrix} \alpha_{11} & ... &\alpha_{1n}\\ ... & ... & ...\\ \alpha_{m1} & ... &\alpha_{mn}\\ \end{bmatrix} \]
根据博弈者\(\alpha\)的支付矩阵,我们可以将该博弈记作 \(G=\{S_\alpha,S_\beta;A\}\)
最优纯策略与纳什均衡
即让自己在的选择在对方从博弈空间中任选博弈时,自己的收益相等。
例:美女硬币
| 男/美女 | 美女正面 | 美女反面 |
|---|---|---|
| 男正面 | 3 -3 | -2 2 |
| 男反面 | -2 2 | 1 -1 |
设男出正面的概率为\(x\),反面的概率为\(1-x\);(女出正面的概率为 y,出反面的概率为\(1-y\))。为使利益最大化,应该在对手出正面或反面的时候自己的收益相等(否则,对方就可以针对):
\[3x + (-2)\times(1-x)=(-2)\times x + 1\times(1-x)\]
有 \(x=3/8\);收益:\(-1/8\)。同理可列方程:
\[-3y+2(1-y) = 2y + (-1)\times(1-y)\]
有 \(y=3/8\);收益:\(1/8\)。
最优混合策略
博弈者只能以一定的概率在策略集中随机地选择每个策略,则这种概率分布被称为混合策略。
令\(x_i\),\(y_i\)为博弈者\(S_\alpha,S_\beta\)在各自策略集中选择\(\alpha_i,\beta_i\)的概率,则称\(x=(x_1...x_m)\)与\(y=(y_1...y_m)\)为两个博弈者的混合策略。
当\(E(x^*,y^*)=v=\min{\max{E(xy)}}=\max{min{E(xy)}}\) 时,称\(x^*,y^*\)为博弈人的最优混合策略(若\(v<0\),则需要给收益矩阵每个元素加上\(d\)使得\(v>0\))
最优混合策略求解方法 可以列出以下两个不等式组
\[ \left\{\begin{array}{lr} \sum_{i=1}^m\alpha_{ij}x_i\ge v\qquad j=1,2,...,n &\\ \sum_{i=1}^m x_i=1 &\\ x_i \ge 0\qquad i=1,2,...,m \end{array} \right. \]
\[ \left\{ \begin{array}{lr} \sum_{j=1}^n\alpha_{ij}y_j\le v\qquad i=1,2,...,m &\\ \sum_{j=1}^n y_i=1 &\\ y_j \ge 0\qquad j=1,2,...,m \end{array}\right. \]
将等式左右同时\(x_i'=\frac{x_i}{v}\),则可以得到线性规划
\[ \min S = \sum^m\_{i=1}x_i' \]
\[ \left\{\begin{array}{lr} \sum_{i=1}^m\alpha_{ij}x_i'\ge v\qquad j=1,2,...,n &\\ x_i' \ge 0\qquad i=1,2,...,m \end{array}\right. \]
和
\[ \min S' = \sum^m\_{i=1}y_i' \]
\[ \left\{\begin{array}{lr} \sum_{j=1}^n\alpha_{ij}y_i'\le 1\qquad i=1,2,...,m &\\ y_i' \ge 0\qquad i=1,2,...,n \end{array} \right. \]
例题,田忌赛马