最大流算法
最近学离散发现网上对于最大流算法介绍的比较少,因此写个 blog 记录一下相关的知识点
最大流
定义一个有向图中的两个顶点分别为源点和汇点,源点入度为 0,汇点出度为 0,每条边有属性最大流量(maximum capacity),表示该边能通过的流量的最大值。我们称该有向图从源点到汇点的最大的流量值即为该图的最大流。
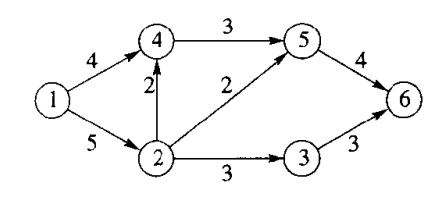
对于如上图的一张图,想要获得从源点 1 到汇点 6 的最大流,我们可以使用如下的朴素算法:
打标签算法(LABELING ALGORITHM)
算法出处:《离散数学结构》P299
算法的思想:将所有边都视为一条实边和一条虚边,其中实边代表我们图中已经给出的方向,而虚边则代表与图中已有方向相反的一条“虚构”的边 (作用在算法中会具体说明),实边和虚边的流量和一定 (一条路的最大流量是不变的)。
步骤:通过类似于 广度优先搜索 的方法 ,每一次确定一条从源点到汇点的最大流,并且每次通过回溯将所有途经过的实边减去这条最大流量,相应的虚边加上最大流量,直到无法再找到一条最后能通过实边抵达汇点的最大流,算法停止。
具体步骤
- 定义一个集合 \(N\) ,其中用于记录当前已经加入的点的集合,最开始将源点
1加入 \(N\)。 - 将最新加入的元素进行延拓至所有可抵达的,且不属于\(N\)中的元素 (先后顺序参照序号) ,对于有向边\(e_{ij}\),如果\(e_{ij}\gt0\),则路径可通 (如果方向和图中路径相反,则考虑虚边是否大于零),第一次则将
1延拓至2 4,并且将其分别标记上\([5,1] [4,1]\) (格式为[可以进入的最大流量, 从哪一个点延拓至该点]) - 将新加入的点加入到 \(N\) 中
- 回到步骤
2,直到 (假设汇点序号为 6) \(6\in N\),记录此时最大的流量 \(f\) - 回溯延拓至汇点的路径,将其对应的实边 \(e_{ij}=e_{ij}-f\),虚边\(e_{ji}=e_{ij}+f\)
- 回到步骤
1,直到无法有路径延拓至汇点