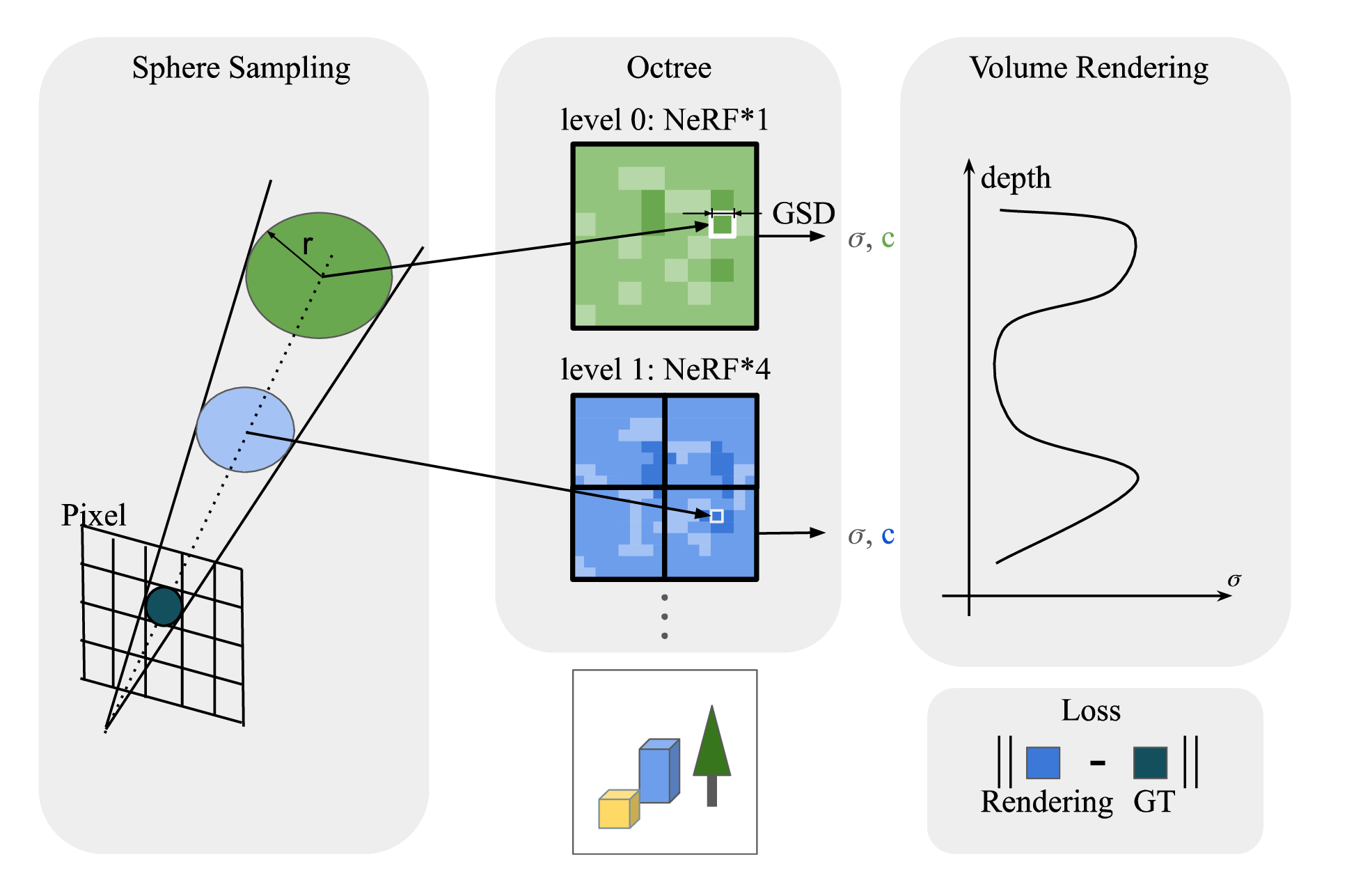
InfNeRF: Towards Infinite Scale NeRF Rendering with O(log n) Space Complexity

用八叉树给 NeRF +NGP 叠上了八叉树，每个八叉树节点再用 2048 的 NGP Nerf，不懂 NeRF，但是看起来像 A+B 的工作

GS^3: Efficient Relighting with Triple Gaussian Splatting

Linear composition of BSDF?

• ROBUST MC Chapter 4 > The operator \(A\) that provides a linear mapping in a vector space \(\mathcal F \rightarrow \mathcal F\) is called a linear operator. \(Af\) denotes the application of an operator to a function, resulting another new function. ### Preliminary Light transport operator: \[ \mathbf T = \mathbf K\mathbf G \tag{1} \]

Where \(\mathbf K\) is the local scattering operator, \(L_o = \mathbf K L_i\), both \(L\) defined in the whole ray space \(\mathcal R\):

\[ (\mathbf Kh)(\mathbf{x}, \omega_o) = \int_{S^2} f_s(\mathbf{x}, \omega_i \to \omega_o) \, h(\mathbf{x}, \omega_i) \, d\sigma_{\mathbf{x}}^\perp(\omega_i) \] \(\mathbf G\) is the propagation operator, defining the geometric property of the space, \(L_i = \mathbf G L_o\), which should be symmetric. \[ (\mathbf Gh)(\mathbf{x}, \omega_i) = \begin{cases} h(\mathbf{x}_M(\mathbf{x}, \omega_i), -\omega_i) & \text{if } d_M(\mathbf{x}, \omega_i) < \infty, \\ 0 & \text{otherwise,} \end{cases} \]

Now right the light transport equation in operator form: \[ L = L_e + \mathbf T L \] Inverting the operator equation: \[ \begin{equation} \begin{aligned} (\mathbf I - \mathbf T)L &= L_e \\ L &= (\mathbf I - \mathbf T)^{-1} L_e \end{aligned} \end{equation} \] Defining solution \(\mathbf S = (\mathbf I - \mathbf T)^{-1}\). Given that \(\Vert \mathbf T \Vert \lt 1\), the inversion can be expanded with Neumann series: \[ \mathbf S = (\mathbf I - \mathbf T)^{-1} = \sum^{\infty}_{i = 0} \mathbf T^i = \mathbf I + \mathbf T + \mathbf T^2+ \cdots \] Light transport can then be expanded as well: \[ L = L_e + \mathbf T L_e + \mathbf T^2 L_e + \cdots \tag{2} \]

前言

经常玩英雄联盟红温的经常玩多人电子竞技游戏的人应该都知道一个游戏匹配机制的重要性。但是很多时候这些迭代多年，理论上应该相当成熟的系统，总是能给我们整个眼前一黑的好活，一局游戏下来完全无法确认你的队友的显示器前坐着的到底是不是智人。

在ACM SIGGRAPH Symposium on Interactive 3D Graphics and Games(I3D) 2024中则有一篇论文Skill-Based Matchmaking for Competitive Two-Player Games介绍了现有机制的缺陷和提出的一种全新匹配系统，笔者出于对队友智力的担忧匹配系统的兴趣，将从该论文出发，讨论现有匹配系统和评分机制。请注意，本文不是对原论文的翻译和直接总结。

什么比赛算好比赛

起因

最近需要在一个2c4g的一个服务器上做VITS-fast-finetuning项目的边缘部署，VITS算一个不大不小的模型，实测下来服务器的内存只有3.6G，刨开乱七八糟的服务也就只剩下少得可怜的2G左右内存可用，因此需要相当地精打细算才能得到比较好的效果。

前端没啥好说的，自己和copilot合作了一下撸了一个又不是不能用的，之后就轮到重量级的后端登场了。

还在漏还在漏

首先我们的需求和一些现实情况如下：

起因

最近在WSL上学习CUDA，不假思索地选择了clangd作为lsp，使用的软件如下：

• Arch WSL2
• CMake 3.28.1
• Cuda compilation tools, release 12.3, V12.3.103
• LLVM 16.0.6
• VSCode 1.85.1

但是使用的过程中，遇到了一个非常神秘的问题，对于C++的源代码*.h和*.cpp等，clangd的代码补全一切正常，但是一遇到.cu文件，completion的延迟会长达几秒钟：

前言

最近在学习写一个离线渲染器的时候，有一个需求是要实时地追踪一条射线逐个打到的物体然后显示debug信息的功能（顺便一说，这个功能真的很好用也很好玩），离线部分仿照的pbrt-v3，交互的前端则是使用的imgui+OpenGL。前面的实现都很顺利，但是到渲染车辆场景的时候，发现射线没有做到指哪打哪，那肯定是出问题了，于是我从头到尾地排查了一遍所有的变换相关的代码。发现了两个问题：

• OpenGL中裁剪空间的Z轴范围要求范围为\([-1, 1]\)，而pbrt的perspective矩阵变换的Z范围为\([0, 1]\)。
• OpenGL需要在NDC之前就考虑viewport的长宽比aspect，但是pbrt将这一步推迟至了cameraToRaster。

进行排查的同时也系统化地解决了大量疑问：

• 老生常谈的MVP矩阵到底是在哪些空间中进行变换？
• 变换的结果范围是什么？
• 用的是左手还是右手坐标系？
• ...

A Realistic Surface-based Cloth Rendering Model

Paper

fiber 纤维，股的组成部分 ply 股（织线的组成） yarn 纺线，n-ply yarn，n股纺线 - ply level 由ply不同的数量、缠绕的方式造成的yarn的不同外观 woven cloth 梭织 - warp-weft 经-纬 knitted cloth 针织 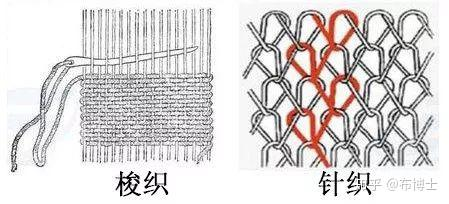- knittet coth 会由于缠绕方式的不同产生体积/阴影遮挡效果，这个层级被称为pattern level

BSDF

输入

首先指路BUPT 计科大三上生存指北 by xqmmcqs，感谢这篇文章给我大三上的课程复习带来了很大的帮助。

碎碎念：为什么会有这篇博客呢？因为我在网上找遍了资料，找到的博客或者复习指南基本都是北邮计科的，这对于小专业的学生来说太不友好了，因此萌生了写一篇和上面提到的文章一样的总结并且希望把这个作为一个习惯传下去（要是懒了就算了罢）。今天是2023年1月8日，正值最后一门成绩出完，因此在这里分享数据科学与大数据技术专业大三上的一些课程的主观感受。

操作系统

难度中上，需要背很多东西，基本是把操作系统的架构底朝天讲了个遍，遗憾或者说庆幸的是每一个内容的深度都不足。xz老师人还不错，今年期中由于封控政策延期了导致最后变成了全是大题，还想得起来的题型有线程调度、信号量之类的；期末则是常规的填空选择大题，复习的话推荐看一遍王道然后刷PPT（注意一些小的知识点，比如今年考了一个文件的访问方式我就写错了orz），大题题型最后都是很常规的PPT例题（今年PV题也不难），把PPT搞懂然后刷往年题就行。

课程附赠一个实验，不过不是单独算的，今年要求2-6人组队，由于已经给出了实验指导书并且书上有源码，本质cv。

首先摘抄一段wiki上对于Perlin噪声的介绍：

Perlin噪声（Perlin noise）指由Ken Perlin发明的自然噪声生成算法。由于Perlin本人的失误，Perlin噪声这个名词现在被同时用于指代两种有一定联系的的噪声生成算法。这两种算法都广泛地应用于计算机图形学，因此人们对这两种算法的称呼存在一定误解。下文中的Simplex噪声和分形噪声都曾在严肃学术论文中被单独的称作Perlin噪声。

接下来，我将围绕生成一张2D噪声纹理为目标展开对于几种噪声生成方法的介绍。

Why

为什么我们需要这两种新的噪声生成方法？对于噪声的生成方法，最为平凡的办法当然是对于每个点取一个均匀分布的随机数，如，生成一个\([0,1]\)的uniform随机数，然后直接将其作为灰度值使用：

奇异递归模板（Curiously Recurring Template Pattern，CRTP）正如其名，是一种递归式利用c++模板的设计模式，更一般地被称作F-bound polymorphism，是我最近在开发数学库的时候听闻的一种惯用法。

What is CRTP?

CRTP的代码很简单，可以用如下的代码演示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

template <typename Child> struct Base {
  void interface() { static_cast<Child *>(this)->implementation(); }
};

struct Derived : Base<Derived> {
  void implementation() { cerr << "Derived implementation\n"; }
};

template <typename ChildType> struct VectorBase {
  ChildType &underlying() { return static_cast<ChildType &>(*this); }
  inline ChildType &operator+=(const ChildType &rhs) {
    this->underlying() = this->underlying() + rhs;
    return this->underlying();
  }
};

父类接收一个子类作为模板参数，子类在实现的时候将自身传入（递归），父类利用这个模板参数将自身静态转换为子类的引用后调用子类的函数。